题目背景

handsomer在城市里游荡，由于他很懒他决定只走最短路，同时由于他人如其名怕被打，经过一条路还需要给驻守该路的恶霸交钱……

题目描述

给定一个每条边有两个参数 (长度len，价值value) 的无向图，请输出\frac{n\times(n-1)}{2}个数表示对于每一组点对(i,j)，他们之间所有长度最短的路径所经过的边构成了一个子图，求该子图的价值和(i< j)

注意：

定义子图的价值和，为该子图所有边的价值的和

如果对于点对(i,j)，没有任何一条路径可以使他们相互到达，则该点对的答案为0

输入格式

第一行两个正整数n,m表示无向图的点数，边数

此后m行，每行4个正整数，表示一条边的两端点，长度len，价值value

输出格式

一行\frac{n\times(n-1)}{2}个数依次表示点对(1,2),(1,3)...(1,n)，(2,3),(2,4)...(2,n)，...，(n-1,n)的答案

样例输入

5 7
1 5 1 1
1 4 2 1
5 4 1 1
5 2 2 1
4 2 1 1
3 4 3 1
2 1 3 1

样例输出

6 4 3 1 2 1 3 1 2 1

样例解释

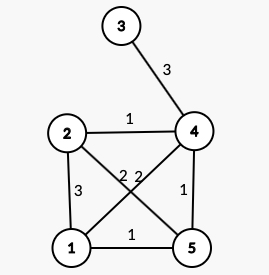
(1,2)的最短路径有：

1->2

1->5->2

1->4->2

1->5->4->2

构成子图的边有：(1,2),(1,5),(1,4),(5,2),(4,2),(5,4)，价值和为6

(1,3)的最短路径有：

1->4->3

1->5->4->3

构成子图的边有：(1,4),(1,5),(5,4),(4,3)，价值和为4

数据范围与约定

对于20\%的数据，保证2\leq n\leq 50

对于另外10\%的数据，保证是一棵树

对于另外10\%的数据，保证0\leq m\leq 10^3

对于100\%的数据，保证2\leq n\leq 300，0\leq m\leq \frac{n\times(n-1)}{2}，1\leq len,value\leq 10^6

保证没有重边和自环